How to Read Math Text in English
How to Read Mathematics
by
Shai Simonson and Fernando Gouvea
Mathematics is �a linguistic communication that can neither be read nor understood without initiation.� ane
A reading protocol is a ready of strategies that a reader must use in guild to benefit fully from reading the text. Verse calls for a different prepare of strategies than fiction, and fiction a dissimilar set than non-fiction. It would be ridiculous to read fiction and enquire oneself what is the author'southward source for the assertion that the hero is blond and tanned; information technology would be wrong to read non-fiction and not ask such a question. This reading protocol extends to a viewing or listening protocol in art and music. Indeed, much of the introductory course material in literature, music and fine art is spent teaching these protocols.
Mathematics has a reading protocol all its ain, and merely as we learn to read literature, we should learn to read mathematics. Students need to learn how to read mathematics, in the aforementioned way they learn how to read a novel or a poem, listen to music, or view a painting. Ed Rothstein�s book, Emblems of Mind, a fascinating book emphasizing the relationship between mathematics and music, touches implicitly on the reading protocols for mathematics.
When we read a novel we become absorbed in the plot and characters. We try to follow the diverse plot lines and how each affects the evolution of the characters. Nosotros make certain that the characters become real people to u.s., both those we admire and those we despise. We practise not stop at every word, but imagine the words equally brushstrokes in a painting. Even if we are not familiar with a particular discussion, nosotros can still run across the whole flick. We rarely stop to call back almost individual phrases and sentences. Instead, we let the novel sweep us along with its flow and carry u.s.a. swiftly to the end. The experience is rewarding, relaxing and thought provoking.
Novelists frequently describe characters by involving them in well-called anecdotes, rather than past describing them by well-chosen adjectives. They portray 1 aspect, then another, then the first once again in a new light and so on, as the whole picture grows and comes more and more into focus. This is the manner to communicate complex thoughts that defy precise definition.
Mathematical ideas are by nature precise and well defined, so that a precise description is possible in a very short space. Both a mathematics article and a novel are telling a story and developing circuitous ideas, merely a math article does the job with a tiny fraction of the words and symbols of those used in a novel. The beauty in a novel is in the aesthetic way information technology uses linguistic communication to evoke emotions and present themes which defy precise definition. The beauty in a mathematics article is in the elegant efficient way it concisely describes precise ideas of great complexity.
What are the common mistakes people make in trying to read mathematics? How tin these mistakes exist corrected?
Don�t Miss the Big Motion-picture show
�Reading Mathematics is not at all a linear experience ...Agreement the text requires cross references, scanning, pausing and revisiting� two
Don�t assume that understanding each phrase, will enable yous to empathise the whole thought. This is like trying to see a portrait painting by staring at each foursquare inch of it from the altitude of your nose. Y'all volition see the particular, texture and colour but miss the portrait completely. A math article tells a story. Try to meet what the story is before you lot delve into the details. You tin go in for a closer await one time you lot have built a framework of understanding. Do this just equally you might reread a novel.
Don�t exist a Passive Reader
�A three-line proof of a subtle theorem is the distillation of years of activeness.
Explore examples for patterns. Endeavor special cases.
A math commodity ordinarily tells only a small piece of a much larger and longer story. The author normally spends months discovering things, and going downward blind alleys. At the end, he organizes it all into a story that covers up all the mistakes (and related motivation), and presents the completed idea in clean slap-up catamenia. The way to really understand the idea is to re-create what the author left out. Read betwixt the lines.
Mathematics says a lot with a piffling. The reader must participate. At every stage, he/she must decide whether or not the idea beingness presented is clear. Ask yourself these questions:
Why is this idea true?
Do I actually believe it?
Could I convince someone else that it is true?
Why didn't the author use a different argument?
Do I accept a better argument or method of explaining the thought?
Why didn't the author explain it the way that I understand it?
Is my way incorrect?
Exercise I really get the idea?
Am I missing some subtlety?
Did this author miss a subtlety?
If I tin't understand the indicate, perhaps I tin understand a similar but simpler idea?
Which simpler idea?
Is it really necessary to understand this idea?
Can I accept this point without agreement the details of why information technology is truthful?
Volition my agreement of the whole story suffer from not understanding why the point is true?
Putting besides niggling effort into this participation is similar reading a novel without concentrating. After half an hr, you wake up to realize the pages have turned, but you have been heedless and don�t remember a thing you read.
Don�t Read Besides Fast
For example, consider the following theorem from Levi Ben Gershon�s manuscript Maaseh Hoshev (The Fine art of Calculation), written in 1321.
�When yous add together sequent numbers starting with 1, and the number of numbers you add together is odd, the issue is equal to the product of the middle number among them times the last number.� It is natural for modern twenty-four hours mathematicians to write this as:
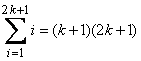
A reader should take every bit much time to unravel the two-inch version every bit he would to unravel the two-sentence version. An case of Levi�s theorem is that 1 + two + 3 + 4 + 5 = iii�5.
Make the Idea your Own
The all-time manner to sympathize what you are reading is to make the idea your own. This means following the idea back to its origin, and rediscovering it for yourself. Mathematicians often say that to empathise something yous must showtime read it, then write it downwards in your own words, then teach it to someone else. Everyone has a different set of tools and a different level of �chunking up� complicated ideas. Make the thought fit in with your ain perspective and experience.
"When I use a word, information technology means just what I choose it to mean"
(Humpty Dumpty to Alice in Through the Looking Glass by Lewis Carroll)
�The meaning is rarely completely transparent, because every symbol or discussion already represents an extraordinary condensation of concept and reference� iv
A well-written math text will exist careful to use a discussion in one sense only, making a distinction, say, betwixt combination and permutation (or arrangement ). A strict mathematical definition might imply that "yellow rabid dog" and "rabid yellowish dog" are different arrangements of words but the aforementioned combination of words. Most English language speakers would disagree. This farthermost precision is utterly foreign to most fiction and poetry writing, where using multiple words, synonyms, and varying descriptions is de rigueur .
A reader is expected to know that an absolute value is not almost some value that happens to be absolute, nor is a function near annihilation functional.
A item notorious example is the use of �Information technology follows hands that� and equivalent constructs. Information technology ways something similar this:
1 can at present check that the adjacent argument is true with a sure amount of essentially mechanical, though peradventure laborious, checking. I, the author, could exercise it, but it would employ upward a large amount of space and peradventure not reach much, since information technology'd be best for you to go alee and do the computation to clarify for yourself what's going on here. I promise that no new ideas are involved, though of class you might demand to think a little in guild to notice just the right combination of skilful ideas to utilise.
In other words, the construct, when used correctly, is a indicate to the reader that what's involved hither is perchance wearisome and fifty-fifty difficult, only involves no deep insights. The reader is then gratis to decide whether the level of understanding he/she desires requires going through the details or warrants saying �Okay, I'll accept your word for it.�
At present, regardless of your stance about whether that construct should be used in a particular situation, or whether authors always use it correctly, you lot should sympathize what it is supposed to mean. �Information technology follows easily that� does not mean
if you lot can�t see this at once, you�re a dope ,
neither does it mean
this shouldn�t take more than than ii minutes ,
but a person who doesn�t know the lingo might interpret the phrase in the incorrect way, and feel frustrated. This is autonomously from the issue that i person�s slow task is another person�s claiming, and so the author must correctly judge the audition.
Know Thyself
Texts are written with a specific audience in listen. Make sure that you are the intended audience, or be willing to do what it takes to become the intended audience.
T.Due south.Eliot�due south
A Song for Simeon:
Lord, the Roman hyacinths are blooming in bowls and
The wintertime sun creeps by the snow hills;
The stubborn flavour has made stand.
My life is light, waiting for the death wind,
Like a feather on the dorsum of my hand.
Dust in sunlight and memory in corners
Wait for the wind that chills towards the dead land.
For instance, Eliot�due south poem pretty much assumes that its readers are going to either know who Simeon was or be willing to discover out. Information technology also assumes that its reader volition be somewhat experienced in reading poetry and/or is willing to work to proceeds such experience. He assumes that they will either know or investigate the allusions hither. This goes beyond noesis of things like who Simeon was. For example, why are the hyacinths �Roman?� Why is that important?
Elliot assumes that the reader will read slowly and pay attending to the images: he juxtaposes dust and memory, relates sometime historic period to winter, compares waiting for death with a plumage on the back of the hand, etc. He assumes that the reader will recognize this equally poetry; in a style, he'south assuming that the reader is familiar with a whole poetic tradition. The reader is supposed to find that alternate lines rhyme, but that the others do not, and then on.
Nigh of all, he assumes that the reader will read not only with the listen, simply also with his/her emotions and imagination, allowing the images to summon upwards this old human being, tired of life but hanging on, waiting expectantly for some crucial event, for something to happen.
Virtually math books are written with assumptions about the audience: that they know certain things, that they have a certain level of �mathematical maturity,� etc. Before you start to read, make sure you know what the writer expects y'all to know.
An Example of Mathematical Writing
To let an opportunity to experiment with the guidelines presented hither, I am including a small piece of mathematics often called the birthday paradox. The first part is a curtailed mathematical article explaining the trouble and solving it. The second is an imaginary Reader's attempt to understand the article by using the appropriate reading protocol. This article�s topic is probability and is attainable to a bright and motivated reader with no background at all.
The Birthday Paradox
A professor in a class of thirty random students offers to bet that at that place are at least 2 people in the class with the aforementioned altogether (month and day, but non necessarily year). Do you have the bet? What if there were fewer people in the class? Would y'all bet then?
Presume that the birthdays of n people are uniformly distributed among 365 days of the year (assume no spring years for simplicity). We prove that, the probability that at least two of them have the same birthday (month and twenty-four hour period) is equal to:
![]()
What is the chance that among 30 random people in a room, there are at to the lowest degree two or more with the same birthday? For n = xxx, the probability of at least 1 matching birthday is about 71%. This means that with 30 people in your class, the professor should win the bet 71 times out of 100 in the long run. It turns out that with 23 people, she should win about 50% of the time.
Hither is the proof: Let P(n) exist the probability in question. Let Q(n) = one � P(north) be the probability that no ii people have a mutual birthday. Now summate Q(north) past computing the number of n birthdays without whatever duplicates and split up by the total number of n possible birthdays. Then solve for P(n).
The total number of n birthdays without duplicates is:
365 � 364 � 363 � ... � (365 � n + ane).
This is because in that location are 365 choices for the first birthday, 364 for the adjacent and and so on for n birthdays. The full number of n birthdays without whatsoever brake is just 365 n because there are 365 choices for each of north birthdays. Therefore, Q(due north) equals
![]()
Solving for P(n) gives P(due north) = 1 � Q(n) and hence our issue.
Our Reader Attempts to Sympathise the Birthday Paradox
In this section, a naive Reader tries to make sense out of the concluding few paragraphs. The Reader�due south part is a metaphor for the Reader thinking out loud, and the Professional�southward comments represent research on the Reader�due south part. The appropriate protocols are centered and bold at various points in the narrative.
My Reader may seem to catch on to things relatively chop-chop. Nonetheless, be assured that in reality a peachy bargain of time passes between each of my Reader�s comments, and that I have left out many of the Reader�due south remarks that explore dead-end ideas. To feel what the Reader experiences requires much more than simply reading through his/her lines. Remember of his/her part as an outline for your own efforts.
Know Thyself
Reader (R): I don�t know annihilation well-nigh probability, can I still brand it through?
Professional (P): Let�s give it a endeavour. We may take to backtrack a lot at each step.
R: What does the phrase �30 random students� mean?
"When I utilize a discussion, information technology means merely what I choose it to mean"
P: Skilful question. Information technology doesn�t mean that nosotros have 30 spacy or scatter-brained people. Information technology means we should assume that the birthdays of these xxx people are independent of one another and that every birthday is equally probable for each person. The author writes this more than technically a little further on: �Assume that the birthdays of northward people are uniformly distributed amidst 365 days of the twelvemonth.�
R: Isn't that obvious? Why bother saying that?
P: Yes the supposition is kind of obvious. The author is just setting the groundwork. The sentence guarantees that everything is normal and the solution does not involve some imaginitive fanciful science-fiction.
R: What do you mean?
P: For example, the author is not looking for a solution similar this: everyone lives in
R: I don�t empathize that long formula, what�south northward?
P: The author is solving the trouble for any number of people, not just for thirty. The author, from now on, is going to call the number of people north.
R: I all the same don't get it. Then what'southward the respond?
Don't Be a Passive Reader - Try Some Examples
P: Well, if you desire the answer for 30, just set n = 30.
R: Ok, merely that looks complicated to compute. Where�south my calculator? Permit�s see: 365 � 364 � 363 � ... � 336. That�s tedious, and the last verbal value won�t fifty-fifty fit on my figurer. It reads:
2.1710301835085570660575334772481e+76
If I can�t even calculate the answer once I know the formula, how tin can I possibly understand where the formula comes from?
P: You lot are right that this answer is inexact, simply if you actually go on and practise the division, your answer won�t be too far off.
R: The whole matter makes me uncomfortable. I would prefer to be able to calculate it more exactly. Is there another way to do the adding?
P: How many terms in your product? How many terms in the product on the bottom?
R: You lot mean 365 is the get-go term and 364 is the 2d? And so there are 30 terms. At that place are likewise 30 terms on the bottom, (30 copies of 365).
P: Can you summate the answer at present?
R: Oh, I see. I can pair up each top term with each bottom term, and do 365/365 every bit the first term, then multiply past 364/365, and and so on for 30 terms. This fashion the product never gets too large for my reckoner. (Subsequently a few minutes)... Okay, I got 0.29368, rounded to 5 places.
P: What does this number hateful?
Don't Miss the Big Picture
R: I forgot what I was doing. Let�s see. I was computing the respond for north = 30. The 0.29368 is everything except for subtracting from 1. If I keep going I get 0.70632. At present what does that mean?
P: Knowing more about probability would help, but this simply means that the take chances that two or more out of the 30 people have the same birthday is 70,632 out of 100,000 or about 71%.
R: That�s interesting. I wouldn�t have guessed that. You hateful that in my course with 30 students, there�s a pretty adept adventure that at least two students have the same birthday?
P: Yes that�s right. You might want to take bets before y'all ask everyone their birthday. Many people don�t think that a indistinguishable will occur. That�s why some authors call this the birthday paradox.
R: So that�s why I should read mathematics, to brand a few extra bucks?
P: I run into how that might requite yous some incentive, but I hope the mathematics also inspires you without the monetary prospects.
R: I wonder what the respond is for other values of n. I will effort some more calculations.
P: That�due south a good idea. We can even make a picture out of all your calculations. We could plot a graph of the number of people versus the take chances that a duplicate altogether occurs, but maybe this tin can be left for another time.
R: Oh look, the author did some calculations for me. He says that for n = 30 the answer is nigh 71%; that�s what I calculated too. And, for northward = 23 it�s about 50%. Does that make sense? I guess it does. The more people there are, the greater the take a chance of a common altogether. Hey, I am anticipating the author. Pretty good. Okay, allow�due south become on.
P: Good, now you lot�re telling me when to go along.
Don�t Read Too Fast
R: Information technology seems that we are up to the proof. This must explicate why that formula works. What�southward this Q(north)? I guess that P stands for probability only what does Q correspond?
P: The author is defining something new. He is using Q only because it�s the next letter of the alphabet subsequently P, simply Q(n) is also a probability, and closely related to P(n). Information technology�s time to take a minute to think. What is Q(n) and why is information technology equal to 1 � P(n)?
R: Q(n) is the probability that no two people have the same altogether. Why does the writer intendance about that? Don�t nosotros want the probability that at least two have the aforementioned birthday?
P: Good point. The author doesn�t tell yous this explicitly, but betwixt the lines, you tin can infer that he has no inkling how to summate P(due north) directly. Instead, he introduces Q(north) which supposedly equals 1 � P(n). Presumably, the author volition continue adjacent to tell us how to compute Q(n). By the way, when you end this commodity, you may want to bargain with the problem of calculating P(n) directly. That�due south a perfect follow up to the ideas presented here.
R: First things first.
P: Ok. So once we know Q(n), then what?
R: And so we tin get P(n). Because if Q(n) = 1 � P(n), then P(n) = 1 � Q(n). Fine, but why is Q(due north) = 1 � P(n)? Does the author presume this is obvious?
P: Aye, he does, but what�southward worse, he doesn�t even tell usa that it is obvious. Hither�due south a rule of thumb: when an author says clearly this is true or this is obvious, then take 15 minutes to convince yourself it is truthful. If an author doesn�t even bother to say this, just only implies it, take a little longer.
R: How will I know when I should stop and think?
P: Just be honest with yourself. When in doubt, stop and recall. When too tired, go lookout man television.
R: So why is Q(n) = 1 � P(due north)?
P: Let�s imagine a special example. If the chance of getting 2 or more of the same birthdays is ane/3, then what's the hazard of non getting two or more?
R: It�southward two/three, because the chance of something not happening is the opposite of the chance of it happening.
Make the Idea Your Own
P: Well, you should be careful when you say things like opposite, merely you are right. In fact, you have discovered one of the first rules taught in a course on probability. Namely, that the probability that something will not occur is ane minus the probability that it will occur. Now go on to the adjacent paragraph.
R: It seems to be explaining why Q(n) is equal to long circuitous-looking formula shown. I will never understand this.
P: The formula for Q(n) is tough to sympathize and the author is counting on your diligence, persistence, and/or background here to get you through.
R: He seems to exist counting all possibilities of something and dividing by the total possibilities, whatever that means. I take no idea why.
P: Maybe I tin fill you in here on some groundwork earlier you endeavor to check out any more details. The probability of the occurrence of a particular type of outcome is defined in mathematics to be: the total number of possible means that blazon of consequence can occur divided by the total number of possible outcomes. For instance, the probability that you throw a four when throwing a die is one/half-dozen. Because at that place is one possible 4, and at that place are six possible outcomes. What'due south the probability you lot throw a four or a three?
R: Well I guess ii/six (or 1/3) considering the full number of outcomes is however 6 but I have 2 possible outcomes that piece of work.
P: Good. Hither�s a harder example. What nigh the chance of throwing a sum of four when you roll 2 die? There are three ways to get a four (1-3, 2-2, iii-1) while the total number of possible outcomes is 36. That is 3/36 or 1/12. Look at the following 6 by 6 table and convince yourself.
i-ane, 1-two, i-3, one-four, 1-5, 1-half-dozen
2-1, 2-ii, 2-3, ii-four, 2-v, 2-half dozen
3-1, 3-2, three-three, three-4, 3-5, 3-6
four-1, four-2, 4-3, 4-4, 4-5, four-6
5-1, five-two, 5-3, 5-4, 5-five, 5-6
half-dozen-1, 6-2, 6-3, 6-4, 6-5, half-dozen-6
What most the probability of throwing a vii?
R: Wait. What does one-i mean? Doesn�t that equal 0?
P: Sorry, my bad. I was using the minus sign as a dash, only to mean a pair of numbers, so one-1 means a roll of 1 on each die - snake eyes.
R: Couldn�t you have come with a better note?
P: Well possibly I could/should take, but commas would look worse, a slash would look similar division, and anything else might be just as confusing. Nosotros aren�t going to publish this transcript anyhow.
R: That�s a relief. Well, I know what you mean now. To reply your question, I tin can get a seven in six ways via 1-6, ii-5, 3-iv, 4-3, five-2, or 6-one. The total number of outcomes is all the same 36, so I get 6/36 or ane/6. That�s weird, why isn�t the chance of rolling a 4 the same as for rolling a seven?
P: Because not every sum is equally likely. The situation would be very dissimilar if we were merely spinning a wheel with the sums 2 through 12 listed in equally spaced intervals. In that case, each one of the eleven sums would accept probability 1/11.
R: Okay, now I am an expert. Is probability just virtually counting?
P: Sometimes, yep. Only counting things is not always so easy.
R: I see, let�due south get on. Past the fashion, did the writer really look me to know all this? My friend took Probability and Statistics and I am not sure he knows all this stuff.
P: There�s a lot of data unsaid in a pocket-sized scrap of mathematics. Yep, the writer expected you to know all this, or to detect it yourself just as we accept washed. If I hadn�t been here, you would have had to ask yourself these questions and answer them by thinking, looking in a reference book, or consulting a friend.
R: So the chance that there are no two people with the same birthday is the number of possible sets of northward birthdays without a duplicate divided by the total number of possible sets of n birthdays.
P: Excellent summary.
R: I don�t similar using northward, so allow me use xxx. Maybe the generalization to n will be easy to see.
P: Great idea. It is frequently helpful to look at a special instance before understanding the general instance.
R: Then how many sets of 30 birthdays are there total? I can�t practice it. I guess I demand to restrict my view fifty-fifty more. Let�due south pretend there are merely two people.
P: Fine. Now y'all�re thinking like a mathematician. Allow�s try due north = two. How many sets of ii birthdays are at that place full?
R: I number the birthdays from 1 to 365 and forget virtually leap years. Then these are the all the possibilities:
1-1, 1-two, one-iii, ... , i-365,
2-1, ii-2, 2-3, ... , ii-365,
...
365-1, 365-2, 365-iii, ... , 365-365.
P: When y'all write 1-1, exercise y'all mean one-1 = 0, as in subtraction?
R: End teasing me. Yous know exactly what I mean.
P: Yes I do, and nice choice of notation I might add. Now how many pairs of birthdays are there?
R: There are 365 � 365 full possibilities for ii people.
P: And how many are there when there are no duplicate birthdays?
R: I tin can�t use 1-1, or 2-ii, or 3-iii or ... 365-365, so I get
i-two, 1-3, ... , 1-365,
2-1, 2-3, ... , ii-365,
...
365-1, 365-ii, ... , 365-364
The total number here is 365 � 364 since each row at present has 364 pairs instead of 365.
P: Practiced. You are going a petty quickly here, merely you lot�re 100% right. Can you generalize now to 30? What is the full number of possible sets of xxx birthdays? Have a guess. You lot�re getting good at this.
R: Well if I had to judge, (it�s not really a guess, afterwards all, I already know the formula), I would say that for 30 people you get 365 � 365 �... � 365, thirty times, for the total number of possible sets of birthdays.
P: Exactly. Mathematicians write 36530. And what is the number of possible sets of 30 birthdays without any duplicates?
R: I know the answer should be 365 � 364 � 363 � 362 � ... � 336, (that is, starting time at 365 and multiply by one less for 30 times), simply I am non sure I really run into why this is truthful. Perhaps I should do the case with 3 people first, and work my way upwardly to 30?
P: Splendid idea. Let�due south quit for today. The whole picture is there for you. When you are rested and yous have more time, you can come back and fill in that last bit of understanding.
R: Thank you a lot; information technology�s been an experience. Later.
two. ibid, folio 16.
3. ibid, page 38
4. ibid, folio 16.
Source: https://www.people.vcu.edu/~dcranston/490/handouts/math-read.html
0 Response to "How to Read Math Text in English"
Post a Comment